さて、ここで突然だが、ＯＰアンプの動作の基礎研究（＾＾；
やはり、電流正帰還アンプを理解するためにはＯＰアンプに帰還を掛けて使う場合のＯＰアンプの挙動を理解しなければならないようだ。

なにせ金田式ＤＣアンプも含めて世のオーディオ用アンプはＯＰアンプＩＣを用いるか否かにかかわらずＯＰアンプだし、この機会だから・・・、などと言えば、「何を今頃」と思われる方もおられれば、パワーアンプまでデジタルになろうとしているのに「今更何を」と思われる方もおられるのでしょうが、まあ、下手な基礎研究と適当に読み飛ばして頂いて、過ちを発見された場合はどうぞご指摘下さい。（＾＾；

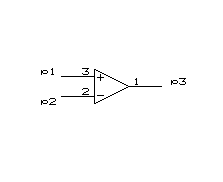ＯＰアンプと言えば“バーチャルショート”、あるいは“イマジナリーショート”と良く言われる。
要するにｐ１とｐ２が仮想的に短絡しているそうだ。
・・・な〜んて（＾＾；、日本語に翻訳して分かったつもりになっても実は何も分からない。

ショートと言われると導線で繋がれているのと同じ状態か・・・と思ってしまうが、そうではない。のだが、まるで繋がっているように考えても良い、という点がバーチャルショートの由来らしいのだが、その意味するところは、ｐ１とｐ２の端子電圧Ｖｐ１とＶｐ２が等しい、即ち、Ｖｐ１＝Ｖｐ２と考えて支障がない。ということらしい。

素人だから、このようにＶｐ１＝Ｖｐ２だよと解説されると、今度は単純にＶｐ１＝Ｖｐ２だという目でＯＰアンプの動作を見てしまうのだが、実際はＶｐ１≠Ｖｐ２であるという冷静かつ沈着な目がないとＯＰアンプの動作は理解できないようでもある。大体、ＯＰアンプを差動動作で使用する場合、ｐ１とｐ２の入力電位差が増幅されて出力されるのだから、Ｖｐ１＝Ｖｐ２の筈がないのだ。

じゃあ、どう考えれば良いの？となるのだが、要するにＶｐ１＝Ｖｐ２と考えて支障がないのだが、Ｖｐ１≠Ｖｐ２である。というのが、バーチャルショートの意味なのだろう。これではますます分からない。う〜ん、そうですね。まあ、マクロに見ればＶｐ１＝Ｖｐ２だが、ミクロに正確に見ればＶｐ１≠Ｖｐ２ということだろうか。実際問題、ｐ１からｐ２に電流がスルーして流れることはない訳で、要するに、マクロに見れば良いときにはＶｐ１＝Ｖｐ２を用い、ミクロに正確に見なければならないときにはＶｐ１≠Ｖｐ２を用いれば良いんだよ、と言うか、用いなければならないんだよ、ということなのだろう。多分（＾＾；

また、ＯＰアンプは理念的には入力インピーダンスは∞、増幅度も∞、出力インピーダンスは０Ωであること、実はそうだからこそバーチャルショートが成り立つのだということ、さらには、非反転入力と反転入力の意味も理解しておく必要があるようだ。

即ち、出力インピーダンスが０Ωということは、出力端子は交流的にはアースと考えて良いと言うこと。素人なので、アースということは電位は０Ｖか、な〜んて思ってしまうのだが、勿論直流的にはそうではなくて、その電位は交流的には非反転入力と同位相、反転入力とは１８０°反転した位相であって、直流的には、非反転入力が＋電位なら出力も＋電位となり、反転入力が＋電位なら出力は−電位になる、というロジックがあるのだ、という理解も必要になる。（なお、図で出力のｐ３端子に極性表示がないが、暗黙の了解で＋ということらしく、省略されている。）

へ〜、じゃあ、直流で非反転入力に＋電位を与え、反転入力にも＋電位を与えたら、出力に現れる電位は＋なんでしょうか？、−なんでしょうか？ロジックの矛盾ではありませんか？　と自ら問うわけだが・・・

う〜ん、その場合は、例の差動動作という考え方を導入して、非反転入力の＋電位＞反転入力の＋電位の場合　→　出力は＋電位で、非反転入力の＋電位＜反転入力の＋電位の場合　→　出力は−電位となり、非反転入力の＋電位＝反転入力の＋電位の場合は　→　勿論出力に変化はなく出力は０Ｖ　となるのですかね。
勿論同相抑圧比なんて言葉があるくらいだから、こういうのは理念的動作で、これは理想のＯＰアンプの場合だ。

まあ、それはともかく、ここでも、バーチャルショートＶｐ１＝Ｖｐ２では差動動作自体理解できないことが分かる訳で、果たしてこの程度の知識で帰還を掛けたＯＰアンプの動作が理解できるのかどうか心許ないが、電流正帰還を少しでも理解するために、ちょっと下手な解析まがいをやってみる・・・の巻（＾＾；

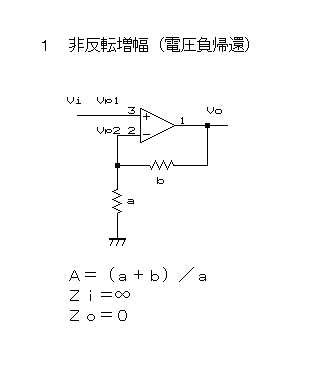
先ずは、１　非反転増幅。ＯＰアンプの増幅動作の典型例として良く見かけるものだ。金田式ＤＣアンプも実はこれだ。

非反転増幅という意味は、入力Ｖｉと出力Ｖｏが同相であるということであり、直流的には入力が＋なら出力も当然＋、入力が−なら出力も−ということだ。
また、このＯＰアンプは理念型のＯＰアンプなので、入力インピーダンスとオープンゲインは無限大、出力インピーダンスは０Ωの理想ＯＰアンプである。

さて、
先ずこの動作でのアンプの増幅率Ａを求めると、
バーチャルショートだから
Ｖｐ１＝Ｖｐ２
ここで　Ｖｐ１＝Ｖｉ、Ｖｐ２＝ａ／（ａ＋ｂ）＊Ｖｏ
よって　Ｖｉ＝ａ／（ａ＋ｂ）＊Ｖｏ
よって　Ｖｏ＝（ａ＋ｂ）／ａ＊Ｖｉ
∴Ａ＝（ａ＋ｂ）／ａ
なので、非反転増幅のクローズドゲインは、帰還ループの抵抗ａとｂにより、（ａ＋ｂ）／ａ　と定まる訳だ。

また、この場合の入力インピーダンスＺｉと出力インピーダンスＺｏは、理想ＯＰアンプの定義から、
Ｚｉ＝∞
Ｚｏ＝０
であることは明らかだ。

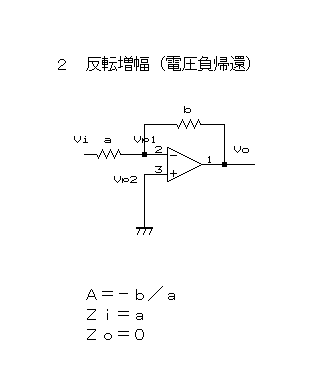次は、２　反転増幅。これの方がＯＰアンプの増幅動作としてはポピュラーらしいが、金田式ＤＣアンプでは差動出力アンプで使われることがあるだけ。ちと違うかな。

反転増幅の意味は、この動作では、入力Ｖｉに対して出力Ｖｏの位相が１８０°反転するということであり、直流的には入力が＋なら出力は−、入力が−なら出力は＋ということだ。

増幅率Ａは、
ここでもバーチャルチャルショートだから　Ｖｐ１＝Ｖｐ２
ここで　Ｖｐ１＝ｂ／（ａ＋ｂ）＊Ｖｉ＋ａ／（ａ＋ｂ）＊Ｖｏ、Ｖｐ２＝０
よって　ｂ／（ａ＋ｂ）＊Ｖｉ＝−ａ／（ａ＋ｂ）＊Ｖｏ
よって　Ｖｏ＝−ｂ／ａ＊Ｖｉ
∴Ａ＝−ｂ／ａ　
なので、反転増幅のクローズドゲインは、−ｂ／ａに定まることになるが、−だから出力の位相は入力と１８０°回転したすなわち反転したものになる訳で、直流入力であれば入力が＋なら出力は−、入力が−ならば出力は＋となる訳だ。

この場合の入力インピーダンスＺｉはどうか。バーチャルショートでＶｐ１＝Ｖｐ２だし、Ｖｐ２はアースに接続されているんだから、Ｖｐ１もアースと考えて、よってＺｉ＝ａ・・・。
・・・まあ、Ｖｐ１＝Ｖｐ２が導線で繋がっている意味であればそうなるが・・・実は自分もさっきまではＺｉ＝aじゃないか、と漠然と思っていたのではあるが・・・（＾＾；；

この場合はａに流れる電流をＩｉとして、Ｚｉ＝Ｖｉ／Ｉｉとして求める。
大体、Ｖｐ１点の入力インピーダンスは∞だから、Ｉｉの電流はＶｐ１点からアースにスルーするはずがなくて、実際はＶｐ１点からｂを通って出力インピーダンスが０Ωの出力端子に抜けると考えるしかないはず。
なので
Ｉｉ＝（Ｖｉ−Ｖｐ１）／ａ＝（Ｖｉ−ｂ／（ａ＋ｂ）＊Ｖｉ−ａ／（ａ＋ｂ）＊Ｖｏ）／ａ＝（ａ／（ａ＋ｂ）＊Ｖｉ−ａ／（ａ＋ｂ）＊Ｖｏ）／ａ＝Ｖｉ／（ａ＋ｂ）−Ｖｏ／（ａ＋ｂ）
ここで　Ｖｏ＝−ｂ／ａ＊Ｖｉを代入して
Ｉｉ＝Ｖｉ／（ａ＋ｂ）＋ｂ／（ａ＊（ａ＋ｂ））＊Ｖｉ＝（ａ＋ｂ）／（ａ＊（ａ＋ｂ））＊Ｖｉ＝Ｖｉ／ａ
∴Ｚｉ＝Ｖｉ／Ｉｉ＝Ｖｉ／（Ｖｉ／ａ）＝ａ

おお！結局バーチャルショートで考えたａじゃないか。
が、それは怪我の功名というもの、か、はたまた、バーチャルショートの功徳なのか・・・（＾＾；

あとは出力インピーダンスＺｏだが、これはＯＰアンプの定義から
Ｚｏ＝０
でいいだろう。

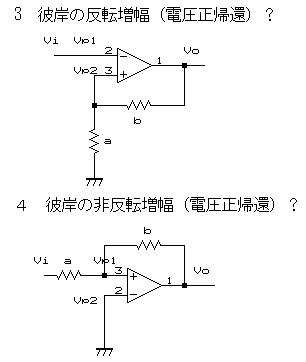
ならば、３　こんなつなぎ方でも動作するのではないか。

この場合でも、バーチャルショートだから　Ｖｐ１＝Ｖｐ２
ここで　Ｖｐ１＝Ｖｉ、Ｖｐ２＝ａ／（ａ＋ｂ）＊Ｖｏ
よって　Ｖｉ＝ａ／（ａ＋ｂ）＊Ｖｏ
∴Ｖｏ＝（ａ＋ｂ）／ａ＊Ｖｉ
∴Ａ＝（ａ＋ｂ）／ａ

なのだが、ロジックで考えると、ａ，ｂは現実の世界の抵抗だからａ，ｂ＞０。従って、Ｖｉが＋なら（ａ＋ｂ）／ａ＊Ｖｉは必ず＋。ところが反転動作のロジックからすればＶｉが＋ならばＶｏは−でなければならない。
よって、この動作は、“−＝＋”というロジックが成り立つ世界でのみ動作する回路だということになる訳で、結局この世では使わない方が賢明な動作のさせ方ということになる。
無理に接続してみたらどうなるか・・・ＯＰアンプもどうしたらよいか途方に暮れて、発狂したり逝ってしまったりするのだろう・・・

続いて　４
これも３と同じく、彼岸のＯＰアンプ動作。
Ａ＝−ｂ／ａ　がロジックに合わない。

なので、彼岸動作のＯＰアンプの考察はこれで終わりにして遂にメインテーマの電流正帰還増幅に進みたい。

が、なんと、それは、上の普通の非反転増幅又は反転増幅のＯＰアンプに、なんとこれらの彼岸のＯＰアンプの動作の形を付加するものなのですなぁ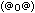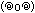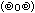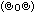

果たしてバーチャルショートで解けるものか？

まず、これ。
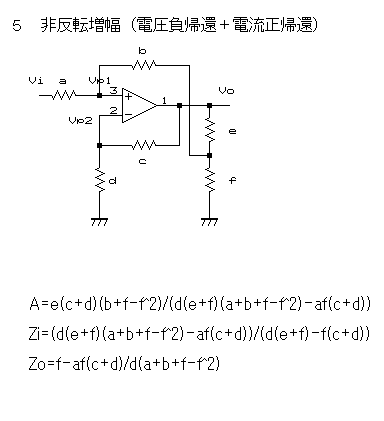
非反転増幅のＯＰアンプが基本となった電流正帰還増幅タイプ。
金田式ＤＣアンプにΛ式ＭＦＢアダプタを付加した場合、こういう回路になる。
ヤマハのＡＳＴのアンプ回路もこうなのかどうかは知らない。

が、これは上の例に比較すると複雑だ。かなり込み入っている。この動作、解析できるだろうか。

まず、この動作でのアンプの増幅率Ａから。
ここでもバーチャルショートだから　Ｖｐ１＝Ｖｐ２
Ｖｐ２＝ｄ／（ｃ＋ｄ）＊Ｖｏ　は良いのだが、問題はＶｐ１。
Ｖｐ１はオームの法則では無理でキルヒホッフの法則を使わないと解けないよう・・・、なのでにわか勉強し（＾＾；；
ａに流れる入力電流をＩｉ、ｅに流れる出力電流をＩｏとすると、
（ａ＋ｂ）・Ｉｉ＋ｆ・（Ｉｉ＋Ｉｏ）＝Ｖｉ
ｅ・Ｉｏ＋ｆ・（Ｉｉ＋Ｉｏ）＝Ｖｏ
これをＩｉについて解くと、
Ｉｉ＝（（ｅ＋ｆ）Ｖｉ−ｆＶｏ）／（（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２））　となる。
Ｉｉが分かれば、Ｖｐ１＝Ｖｉ−ａ＊Ｉｉ　だから
Ｖｐ１＝Ｖｉ−（（ｅ＋ｆ）Ｖｉ−ｆＶｏ）／（（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２））＊ａ
　　　＝（ｂ＋ｆ−ｆ＾２）／（ａ＋ｂ＋ｆ−ｆ＾２）＊Ｖｉ＋ａｆ／（（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２））＊Ｖｏ
となる。
ここで
Ｖｐ２＝ｄ／（ｃ＋ｄ）＊Ｖｏ、バーチャルショートでＶｐ１＝Ｖｐ２　だから
ｄ／（ｃ＋ｄ）＊Ｖｏ＝（ｂ＋ｆ−ｆ＾２）／（ａ＋ｂ＋ｆ−ｆ＾２）＊Ｖｉ＋ａｆ／（（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２））＊Ｖｏ
よって　
ｄ／（ｃ＋ｄ）＊Ｖｏ−ａｆ／（（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２））＊Ｖｏ＝（ｂ＋ｆ−ｆ＾２）／（ａ＋ｂ＋ｆ−ｆ＾２）＊Ｖｉ
よって
Ｖｏ＝（ｃ＋ｄ）（ｅ＋ｆ）（ｂ＋ｆ−ｆ＾２）／（ｄ（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））＊Ｖｉ
∴Ａ＝（ｃ＋ｄ）（ｅ＋ｆ）（ｂ＋ｆ−ｆ＾２）／（ｄ（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））
としたいところだが、ここで、Ｖｉ、Ｖｐ１、Ｖｐ２、Ｖｏは全て対アース電圧であることに留意する必要がある。何故なら、この型式で出力を取り出すのは、Ｖｏとアース間ではなく、抵抗ｅ（＝スピーカー）の両端だ。
だからこの場合の正しい出力Ｖｏ’は
Ｖｏ’＝（ｃ＋ｄ）（ｅ＋ｆ）（ｂ＋ｆ−ｆ＾２）／（ｄ（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））＊Ｖｉ＊ｅ／（ｅ＋ｆ）
　　 ＝ｅ（ｃ＋ｄ）（ｂ＋ｆ−ｆ＾２）／（ｄ（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））＊Ｖｉ
∴Ａ＝ｅ（ｃ＋ｄ）（ｂ＋ｆ−ｆ＾２）／（ｄ（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））
と、何とか求まったようだ。（＾＾）

じゃあ、入力インピーダンスＺｉはどうか。
Ｚｉ＝Ｖｉ／Ｉｉ　に違いあるまい。で、Ｉｉはすでに求めてある。
Ｉｉ＝（（ｅ＋ｆ）Ｖｉ−ｆＶｏ）／（（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）
ここで、Ｖｏ＝（ｃ＋ｄ）（ｅ＋ｆ）（ｂ＋ｆ−ｆ＾２）／（ｄ（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））＊Ｖｉ　を代入して、
Ｉｉ＝（ｄ（ｅ＋ｆ）−ｆ（ｃ＋ｄ））／（ｄ（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））＊Ｖｉ
ここでＺｉ＝Ｖｉ／Ｉｉだから
Ｚｉ＝（ｄ（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））／（ｄ（ｅ＋ｆ）−ｆ（ｃ＋ｄ））
と、入力インピーダンスも求まった。

最後に出力インピーダンスだが、これはいくら考えてもバーチャルショートの考え方だけでは求められないよう・・・
どうすれば求められるのか・・・・・・
と、ややしばらく途方に暮れて、断念しかかった。

が、Ａ＝ｅ（ｃ＋ｄ）（ｂ＋ｆ−ｆ＾２）／（ｄ（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））を眺めているうちに、ふと、ＯＮ−ＯＦＦで求めてはどうか、と考えついた。（＾＾）
と言って、開放時と負荷時のＶｏの差で求めるのではなくて、負荷Ｒ１とＲ２（Ｒ１＜Ｒ２とする）を用意して、Ｒ１負荷時の出力電圧とＲ２負荷時の出力電圧から出力インピーダンスを求める方法で、Ｒ１負荷時の出力電圧をＶｏ１、Ｒ２負荷時の出力電圧をＶｏ２、出力インピーダンスをＺｏとすれば、ＯＰアンプ本来の起電力（Ｖとする）がＺｏとＲ１又はＲ２で分圧されてＶｏ１又はＶｏ２の出力電圧となると考えれば良い筈なので、従って、Ｖｏ１＝Ｒ１／（Ｚｏ＋Ｒ１）＊Ｖ、Ｖｏ２＝Ｒ２／（Ｚｏ＋Ｒ２）＊Ｖ　だから
（Ｒ１＋Ｚｏ）＊Ｖｏ１／Ｒ１＝（Ｒ２＋Ｚｏ）＊Ｖｏ２／Ｒ２
これをＺｏについて解くと、
Ｚｏ＝Ｒ１＊Ｒ２＊（Ｖｏ２−Ｖｏ１）／（Ｒ２＊Ｖｏ１−Ｒ１＊Ｖｏ２）　で出力インピーダンスが求められる。
だから、Ｒ２＝２Ｒ１を満たしている時（８Ωと１６Ωとか４Ωに８Ωとか）には
Ｚｏ＝２＊Ｒ１＊（Ｖｏ２−Ｖｏ１）／（２＊Ｖｏ１−Ｖｏ２）　で出力インピーダンスが求められることになる。

という手法をここで適用しようという考えだ。

が、問題は、こんな机上のアンプの出力インピーダンスを計算しようというのに、外から抵抗をあててＶｏを測る訳にもいくまいに、その考え方を適用できるのか、なのだが、
この電流出力アンプ、負荷がｅそのもので、Ｖｏ’は上のとおりｅの関数でもある、というところが肝だ。（＾＾）
であれば、このアンプの出力インピーダンスは机上のＯＮ−ＯＦＦ法で求められる筈だ。
と、早速やってみれば・・・、

２ｅ時のＶｏ’＝２ｅ（ｃ＋ｄ）（ｂ＋ｆ−ｆ＾２）／（ｄ（２ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））＊Ｖｉ
ｅ時のＶｏ’＝ｅ（ｃ＋ｄ）（ｂ＋ｆ−ｆ＾２）／（ｄ（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））＊Ｖｉ
よって、
Ｚｏ＝（２ｅ（２ｅ（ｃ＋ｄ）（ｂ＋ｆ−ｆ＾２）／（ｄ（２ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））＊Ｖｉ−ｅ（ｃ＋ｄ）（ｂ＋ｆ−ｆ＾２）／（ｄ（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））＊Ｖｉ））／（２ｅ（ｃ＋ｄ）（ｂ＋ｆ−ｆ＾２）／（ｄ（ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））＊Ｖｉ）−２ｅ（ｃ＋ｄ）（ｂ＋ｆ−ｆ＾２）／（ｄ（２ｅ＋ｆ）（ａ＋ｂ＋ｆ−ｆ＾２）−ａｆ（ｃ＋ｄ））＊Ｖｉ）

これを整理すると
Ｚｏ＝ｆ−ａｆ（ｃ＋ｄ）／ｄ（ａ＋ｂ＋ｆ−ｆ＾２）
なんと。求まった。
実に単純な式になるものだ。
ふ〜む・・・、ｅが消えてしまう。
ということは、この回路の出力インピーダンスは、ｅ（＝即ちスピーカーのインピーダンス）に関係しない訳だ。
が、ｅは現実のスピーカーである訳で、こちらの都合で取り替えたりしたい訳だから、出力インピーダンスが負荷のスピーカーのインピーダンス（＝ｅ）の影響を受けないなら、その方が良いに決まっている。（＾＾）

さて、以上は解析のアルゴリズムが正しい場合にだけ正しいものだ。アルゴリズムに誤りがあった場合はなんら意味のない話になるが・・・、ま、早速、ａ，ｂ，ｃ，ｄ，ｅ，ｆに実際の数値を入れてコンピュータに計算させてみよう。（＾＾；

a	10k	10k	10k	10k	10k	10k	10k	10k	10k	10k	10k	10k	10k
b	50k	40k	30k	20k	10k	8k	6k	4k	2k	1k	500	100	0
c	6.8k	6.8k	6.8k	6.8k	6.8k	6.8k	6.8k	6.8k	6.8k	6.8k	6.8k	6.8k	6.8k
d	680	680	680	680	680	680	680	680	680	680	680	680	680
e	8	8	8	8	8	8	8	8	8	8	8	8	8
f	0.22	0.22	0.22	0.22	0.22	0.22	0.22	0.22	0.22	0.22	0.22	0.22	0.22
電圧ゲイン（倍）	9.38	9.10	8.67	7.91	6.28	5.69	4.92	3.87	2.36	1.33	0.71	0.15	0.00
〃（ｄｂ）	19.44	19.18	18.76	17.96	15.96	15.10	13.84	11.75	7.46	2.48	-2.97	-16.48
入力ｲﾝﾋﾟｰﾀﾞﾝｽ（Ω）	80.9k	66.7k	52.5k	38.3k	24k	21.3k	18.5k	15.7k	12.8k	11.4k	10.7k	10.1k	10k
出力ｲﾝﾋﾟｰﾀﾞﾝｽ（Ω）	-0.18	-0.26	-0.38	-0.59	-0.99	-1.12	-1.29	-1.51	-1.80	-1.98	-2.08	-2.18	-2.20

これは、電池式ＧＯＡパワーアンプにΛ式ＭＦＢアダプタを装着して電流正帰還量調整抵抗（＝ｂ）を絞っていくイメージのシミュレーション。

正帰還量調整抵抗（＝ｂ）を絞るということは、正帰還を徐々に増やすことなのだが、そうした場合、
（イ）　アンプの電圧ゲインは徐々に減少し、ｂ＝０の時に電圧ゲインも０になる。
（ロ）　入力インピーダンスは徐々に減少に、ｂ＝０の時に最低値となる。その時の入力インピーダンスはａとなる。
（ハ）　出力インピーダンスは負であり、その値は正帰還量を増やすとともに増加し、その最大値はｂ＝０の時の−２．２オームである。
となることが分かる。

	１	２	３	４	５	６	７	８	９	１０	１１
a	10k	10k	10k	10k	20k	10k	10k	10k	10k	20k	10k
b	50k	50k	50k	50k	50k	50k	50k	50k	50k	50k	50k
c	6.8k	10k	6.8k	6.8k	6.8k	6.8k	6.8k	6.8k	6.8k	6.8k	6.8k
d	680	1k	680	680	680	680	680	330	330	330	330
e	8	8	8	8	8	16	4	8	8	8	1
f	0.22	0.22	0.47	0.11	0.22	0.22	0.22	0.22	0.47	0.47	0.47
電圧ゲイン（倍）	9.38	9.38	9.64	9.27	8.35	9.27	9.61	19.39	21.25	22.17	-80.93
〃（ｄｂ）	19.44	19.44	19.68	19.34	18.43	19.34	19.65	25.75	26.66	26.92
入力ｲﾝﾋﾟｰﾀﾞﾝｽ（Ω）	80.9k	80.9k	138.3k	68.8k	90.9k	68.8k	127.2k	128.6k	-241.4k	-231.4k	1.5k
出力ｲﾝﾋﾟｰﾀﾞﾝｽ（Ω）	-0.18	-0.18	-0.39	-0.09	-0.47	-0.18	-0.18	-0.57	-1.22	-2.43	-1.22

次は、ｂを固定して、他の抵抗の変化がどういう結果をもたらすかの概観。
１が上の状態として、

２は、ｃ、ｄ即ち負帰還抵抗を変化させてみたものだが、その比率が同じであれば、ｂ、ｃの変化は結果に何らの影響も与えないことが分かる。

３、４はｆ、即ち電流検出抵抗を変化させてみたものだが、まず、出力インピーダンスがｆに大体比例することが分かる。よって、ｆに大きな抵抗値の抵抗を持ってくれば、簡単に大きな負性インピーダンスが得られる訳だ。また、入力インピーダンスもｆが大きい方が大きくなることも分かる。また、影響は小さいが、ｆの大小が電圧ゲインにも影響し、ｆが大きいとゲインも大きくなることが分かる。

５はａを大きくしてみたものだが、結果負性出力インピーダンスが大きくなるから、大きな負性インピーダンスを得る方法としてａを大きくすることもかなり有効であることが分かる。併せて入力インピーダンスも大きくなっているが、電圧ゲインはやや小さくなってしまう。

６，７はｅ（＝スピーカー）を変えて見たものだが、確かに出力インピーダンスはｅの値によって変化しないが、入力インピーダンスがｅ（＝スピーカーのインピーダンス）に反比例してかなり大きく変化することは気になる点だ。また、電圧ゲインはｅが小さい方が大きくなっており、しかもその増加ペースがｅの減少に比例ではなく、減少に加速して増加している。これはかなり恐ろしい結果を予測させる現象なのだが、とりあえず置いておいて次にいくと、

８、９はｃとｄの比率を変えて、電圧ゲインを上げてみようとしたものだ。計算結果も電圧ゲインは大きくなっている。そして、電圧ゲインを大きくすることも負性インピーダンスを大きくし、入力インピーダンスを大きくする方向に作用することがわかる。
が、９で、これまでの解析結果からさらにｆも大きくして一層大きな負性インピーダンスを得ようとしたところ、なんと入力インピーダンスまで負性インピーダンスになってしまうではないか。

１０は、さらにａも大きくしたもの。負性の出力インピーダンスは一層大きくなり、入力インピーダンスはやはり負性である。
入力インピーダンスが負性という状態は、現実にもあり得る状態ではないかと考えられるが、この状態で果たしてまともに動作するものかどうかは良く分からない。

で、１１が電流正帰還アンプが破綻を秘めたアンプであることを示す状態だ。
７で、eを小さくするほどに電圧ゲイン（＝出力電力）が加速して大きくなることを見たのだが、そうやって電圧ゲインを大きくなるようにｅを小さくしてみると、電圧ゲインが−になってしまうのだ。
が、入出力間のロジックを考えると、この場合は入力Ｖｉが＋の時は出力Ｖｏは＋でなければならないから、この状態は論理矛盾に陥った状態だ。実際はどうなるのか？彼岸のＯＰアンプ動作に至ってしまうということだが、端的に言えば発振？だろうか。

やはり電流正帰還はむやみに試してみるものではない。下手をすれば発振に至るのだ。それはΛ式ＭＦＢアダプタを既存アンプに取り付けた場合も同じだ。アンプが発振してアンプを壊したり、スピーカーを飛ばしたりするリスクに耐えられる人以外は作ったり、使ったりしてはいけないのだ。

ま、逆に言えば以上のリスクを管理できる方が自己責任で作ったり使ったりする分には何ら問題がないわけだ。
が、その場合のこの回路構成による電流正帰還の問題点、というか、使いにくい点は、負性インピーダンスの大きさと、電圧ゲイン及び入力インピーダンスが反比例関係である点だろう。入力インピーダンスの低さはこの程度なら普通は問題ないのだが、残念なことに金田式パッシブチャンネルデバイダーの使用を考えると無理なのだ。どうしてもバッファアンプが必要になってしまう。実はこの点が、反転増幅型の電流正帰還アンプの製作を考えた理由であるわけで・・・。
ゲインの減少は、負性インピーダンスを欲張らなければ、取りあえずなんとかなるレベルだとは思うが・・・

負性インピーダンスの大きさと、アンプの電圧ゲイン＆アンプの入力インピーダンスの高さを両立出来ないか、と考えたのが今回製作したアンプで、それが次の回路構成だ。

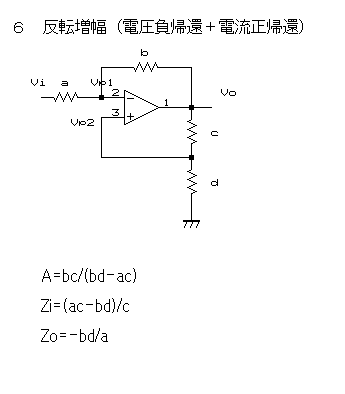
これは、上の反転増幅型に彼岸のオペアンプ動作を付加したものとでも言えるだろうか。
世の中では、発振器なんかでこういう帰還のつなぎ方をしているようだ。私もようやく認識したのだが、Ｋ式ターンテーブル制御アンプで使われているウィーンブリッジ発振回路がこの構成で、要するに発振器用の回路構成なのだ。果たしてこれを上手く活用して期待に応える電流正帰還アンプが構成できるのだろうか。

ここでもバーチャルショートで、Ａから求めると、
Ｖｐ１＝Ｖｐ２
Ｖｐ１＝ｂ／（ａ＋ｂ）＊Ｖｉ＋ａ／（ａ＋ｂ）＊Ｖｏ
Ｖｐ２＝ｄ／（ｃ＋ｄ）＊Ｖｏ
よって、ｂ／（ａ＋ｂ）＊Ｖｉ＝（ｄ／（ｃ＋ｄ）−ａ／（ａ＋ｂ））＊Ｖｏ
∴Ｖｏ＝（ｂｃ＋ｂｄ）／（ｂｄ−ａｃ）＊Ｖｉ
∴Ａ＝（ｂｃ＋ｂｄ）／（ｂｄ−ａｃ）
となるのだが、ここでもこの型式の出力の取り出し口はｃの両端であることに留意して
Ｖｏ’＝（ｂｃ＋ｂｄ）／（ｂｄ−ａｃ）＊Ｖｉ＊ｃ／（ｃ＋ｄ）＝ｂｃ／（ｂｄ−ａｃ）＊Ｖｉ
∴Ａ＝ｂｃ／（ｂｄ−ａｃ）

う〜む。上に比して実に単純ではないか。分かりやすい。

この構成ではＶｉとＶｏは反転動作だが、ＶｉとＶｏが反転動作であるというロジックが成立するためにはＡは−でなければならない筈である。ａ，ｂ，ｃ，ｄは現実界の抵抗だから、すべて正数である。だから、ｂｃ／（ｂｄ−ａｃ）が負であるために、ａｃ＞ｂｄであることが必須の条件になる。

もし、ａｃ＜ｂｄという定数設定にしたらどうなるのか。それは多分彼岸のＯＰアンプ動作で、現実としては破綻＝発振に至ることが予想される。恐ろしや〜で、この構成のアンプもアンプが発振してアンプを壊したり、スピーカーを飛ばしたりするリスクに耐えられる人以外は作ったり、使ったりしてはいけないのだ。

が、逆に言えばａｃ＞ｄｂを満たすように定数設定すれば良いのだ。実に簡単なリスク管理であり、５の非反転増幅方式ではこの点の式がちょっと複雑で、どこが限界なのかが簡単には計算できないのに対してこちらは限界計算、結局、限界管理がしやすいのは大きなメリットだ。と言えるだろう。

次に入力インピーダンスＺｉだが、
Ｉｉ＝（Ｖｉ−Ｖｐ１）／ａ　に　Ｖｐ１＝ｂ／（ａ＋ｂ）＊Ｖｉ＋ａ／（ａ＋ｂ）＊Ｖｏ＝（ｂ＊Ｖｉ＋ａ＊Ｖｏ）／（ａ＋ｂ）を代入し
Ｉｉ＝（Ｖｉ−Ｖｏ）／（ａ−ｂ）
ここで　Ｖｏ＝（ｂｃ＋ｂｄ）／（ｂｄ−ａｃ）＊Ｖｉを代入すると
Ｉｉ＝ｃ／（ａｃ−ｂｄ）＊Ｖｉ　だから
Ｚｉ＝（ａｃ−ｂｄ）／ｃ
となる。
ここでもａｃ＜ｂｄという設定にしたらＺｉ即ち入力インピーダンスが−、即ち負性インピーダンスになるということ。だが、ａｃ＜ｂｄはこの構成のアンプでは破綻条件だから、ここで単独に入力インピーダンスが負性といったところで何の意味もない。動作の破綻と共に入力インピーダンスが計算上負性になるということだ。

次は出力インピーダンスＺｏ
ちょっと見ると、Ｚｏ＝０ではないのだろうか、と思える。バーチャルショートで考えるということは、このＯＰアンプが理想ＯＰアンプということだ。だからＺｏ＝０Ω。それがＦＢをちょっといじったぐらいで変わるのだろうか？

実は、もとより出力をＶｏとアース間で取り出せばそうなのだが、出力をｃの両端で取り出すというのがこれに限らず電流出力タイプのアンプを考える上でのミソだ。
で、これもＯＮ−ＯＦＦ法で計算して、
２ｃ時のＶｏ’＝２ｂｃ／（ｂｄ−２ａｃ）
ｃ時のＶｏ’＝ｂｃ／（ｂｄ−ａｃ）
従って
Ｚｏ＝２ｃ（２ｂｃ／（ｂｄ−２ａｃ）−ｂｃ／（ｂｄ−ａｃ））／（２ｂｃ／（ｂｄ−ａｃ）−２ｂｃ／（ｂｄ−２ａｃ））
整理して、な〜んと！
Ｚｏ＝−ｂｄ／ａ
となるのである。

ここでも出力インピーダンスは帰還抵抗ａ，ｂ，ｄのみで決まって、ｃ（＝スピーカーのインピーダンス）が影響しない。
しかも、ａ，ｂ，ｄは現実界の抵抗で即ち正数だから、出力インピーダンスは、はなから負性インピーダンスになることに決まっているのだ。

ところで、−ｂ／ａはどこかにあった。上に方で見た２　反転増幅（電圧負帰還）の場合の増幅率Ａそのものだ。出力インピーダンスが、そもそもの反転増幅の形の場合の増幅率に電流検出抵抗ｄを乗じた数値に決まるとは実に面白い。

a	51k	51k	51k	51k	51k	51k	51k	51k	51k	51k	51k	51k
b	560k	560k	560k	560K	560k	560k	560k	560k	560k	820k	820k	820k
c	4	4	4	8	8	8	16	16	16	8	8	8
d	0.11	0.22	0.47	0.11	0.22	0.47	0.11	0.22	0.47	0.11	0.22	0.47
電圧ゲイン（倍）	-15.73	-27.72	37.84	-12.93	-15.73	-30.94	-11.88	-12.93	-16.21	-20.64	-28.82	-290.27
〃（ｄｂ）	-23.93	-28.86		-22.23	-23.93	-29.81	-21.5	-22.23	-24.2	-26.29	-29.19	-49.26
入力ｲﾝﾋﾟｰﾀﾞﾝｽ（Ω）	35.6k	20.2k	-14.8k	43.3k	35.6k	18.1k	47.2k	43.3k	34.6k	39.7k	28.5k	2.8k
出力ｲﾝﾋﾟｰﾀﾞﾝｽ（Ω）	-1.21	-2.42	-5.16	-1.21	-2.42	-5.16	-1.21	-2.42	-5.16	-1.77	-3.54	-7.56

これが、今回製作した電流正帰還・電池式完全対称型ＤＣアンプをイメージしたシミュレーションだ。
これを眺めると、反転型の電流正帰還アンプが非反転型のそれに比べると分かりやすさと融通性でかなり優れるように思うのだが、結論として、６〜８Ωのスピーカーを対象とした場合、ａ＝５１ｋ、Ｂ＝５６０Ｋ、ｄ＝０．２２Ωというのが１つの良い解であるように思えるがどうだろう。

こちらの方式は、上の方式に対して、電流正帰還量を増やすほどに電圧ゲインが減ってしまうということがないので、大きな負性インピーダンスを得ることはより易しい。Ｚｏ＝−ｂｄ／ａだから、ｂ、ｄを大きくするか、ａを小さくすれば良いのだ。

が、負帰還量を考えれば、ａ，ｂではなく、ｄで調整すべきだ。というと調整範囲が狭いように感じてしまうが、実際は上の表のようにｄで出力の負性インピーダンスは大きく調整できるのだ。

が、あまり大きくするのは妥当でない。上の表の左から３番目のように、出力インピーダンスとｃ（＝スピーカーのインピーダンス）の合計値が負になるような状態では、ＶｉとＶｏのロジックがすでに不整合であるから、これはもう破綻した動作だ。
スピーカーのインピーダンスが周波数によって公称の半分程度に下がる部分があることを考慮すれば、負性出力インピーダンスの絶対値は、使用するスピーカーの公称インピーダンス値の１／３〜１／４程度に押さえるのが妥当のように思う。

ところで、上で述べたとおり、この方式については入力インピーダンスも高い値が得られることを期待したのだ。
が、残念ながら入力インピーダンスが下がってしまうのはこの方式も同じだった。
とはいえ、得られる電圧ゲインと負性インピーダンスの大きさを考えると、こちらの反転増幅方式の方が比較すれば高い入力インピーダンスが得られるので、とりあえず良しとすべきだろう。実際３６ＫΩの入力インピーダンスが得られれば、低音側フィルターでそのｆｃが移動しても何とか使えないこともないのだ。私の駄耳では（＾＾；

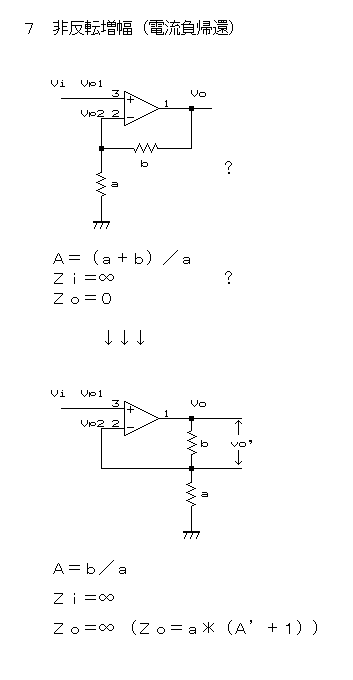最後に、電流負帰還についても考察してみよう。
それが、右だ。
え、最初の非反転増幅と全く同じではないか？
実はそうなのだが、まあ、解析してみれば、

この動作でのアンプの増幅率Ａも、
バーチャルショートだから　Ｖｐ１＝Ｖｐ２
ここで　Ｖｐ１＝Ｖｉ、Ｖｐ２＝ａ／（ａ＋ｂ）＊Ｖｏ
よって　Ｖｉ＝ａ／（ａ＋ｂ）＊Ｖｏ
よって　
Ｖｏ＝（ａ＋ｂ）／ａ＊Ｖｉ
と、ここまでは最初の非反転増幅と同じだが、ここで、電流負帰還アンプとして使用する場合は、その出力はｂの両端から取り出すことに留意しなければならない。
だから、電流負帰還の場合の正しい出力Ｖｏ’は
Ｖｏ’＝Ｖｏ×ｂ／（ａ＋ｂ）＝（ａ＋ｂ）／ａ＊Ｖｉ＊ｂ／（ａ＋ｂ）
よって
Ｖｏ’＝ｂ／ａ＊Ｖｉ
∴Ａ＝ｂ／ａ
となる。

入力インピーダンスＺｉは、ＯＰアンプの定義からして、
Ｚｉ＝∞
であることは明らかだ。

では、出力インピーダンスはどうか。
ＯＮ−ＯＦＦ法で求めよう。この場合はｂが即ち負荷（スピーカー）だから、
Ｚｏ＝２＊Ｒ１＊（Ｖｏ２−Ｖｏ１）／（２＊Ｖｏ１−Ｖｏ２）に
２ｂ時のＶｏ’＝２ｂ／ａ＊Ｖｉ
ｂ時のＶｏ’＝ｂ／ａ＊Ｖｉ
を代入して、
Ｚｏ＝２ｂ（２ｂ／ａ＊Ｖｉ−ｂ／ａ＊Ｖｉ）／（２ｂ／ａ＊Ｖｉ−２ｂ／ａ＊Ｖｉ）
なんと、分母が０となってしまうので、コンピューターではDＩV／０！　エラー　になるのだが、実はエラーではなくて、その意味は、
Ｚｏ＝∞
なのである。

要するに、バーチャルショートが完璧に成り立つＯＰアンプとは、即ちオープンゲイン∞、入力インピーダンス∞、出力インピーダンス０Ωの理想状態であるから、この非反転動作負帰還アンプは、Voとアースの出力インピーダンスが０Ωであるが故に、これをｂ両端から出力を取り出す電流負帰還アンプとして使用した場合は、出力インピーダンスが∞になる、という表裏一体の関係なのだ、ということだろう。

が、この世界は理想的ではないので理想ＯＰアンプも現実には存在しない。現実に存在するＯＰアンプのオープンゲインは有限だ。その場合の出力インピーダンスはどうなるのだろう。
という点は“Ｗｈａｔ’ｓ　ＵＴｉＣｄ？”氏のＨＰに解があって、ＯＰアンプのオープンゲインをＡ’として、Ｚｏ＝ａ＊（Ａ’＋１）となるそうだ。
例えば、ａ＝０．２２Ωとして、Ａ’＝６０ｂｄ（１０００倍）であれば、２２０Ωの出力インピーダンスとなるわけだ。

が、この型式で安定に動作するアンプを作ることは現実的ではないだろう。この型式ではスピーカーを取り付けないとアンプには負帰還がかからない。だから現実的にスピーカーと一体型のアンプしか作れないだろうから、汎用性のあるアンプにはならない。

また、極めて高い出力インピーダンスがスピーカードライブにとって有益なのかどうか。これは高出力インピーダンスの電流出力アンプを製作される方もいらっしゃるのでなんとも言えないが、通常は電圧負帰還と電流負帰還を併用して、適度な正の出力インピーダンスに設定するために活用するということではないだろうか。そして、それを最も単純な形で実現している例が実は金田式ＭＦＢだ、ということになるのだ。（ところで、Ｋ式ＭＦＢ方式の出力インピーダンスも多分計算が可能だと思うのだが、ここではやらない。）

（２００２．５．１３）

（続きはこちらへ）